Chiffrement et hash en PHP contre l'attaque Man in the middle

V-A-1. Chiffrement symétrique▲

V-A-2. Chiffrement asymétrique▲

Nous allons ici voir comment chiffrer une donnée provenant d'un formulaire utilisateur.
Tout d'abord, il convient de bien situer le but.
Je rappelle que cette partie concerne les données que l'on souhaite chiffrer côté client afin de ne pas les faire circuler sur le réseau en clair, mais qu'un hash n'est pas possible, car nous avons besoin de cette donnée en clair côté serveur.
Chronologiquement, ça va se dérouler de la sorte.

Déroulement du chiffrement asymétrique d'une donnée distante

• Le serveur génère une paire de clés publique/privée.
• Il garde la clé privée (en session ou en base).
• Il envoie la clé publique avec le formulaire demandant la donnée à chiffrer.
• On chiffre côté client en utilisant la clé publique.
• On envoie le formulaire contenant uniquement la donnée chiffrée (on retire évidemment celle saisie par l'utilisateur en clair).
• On déchiffre côté serveur avec la clé privée pour récupérer notre donnée.

Nous avons donc besoin de générer la paire de clés en PHP, de chiffrer en Javascript et de déchiffrer en PHP.

Côté PHP

Pour la partie PHP, nous utilisons le package Crypt_RSA (version 1.2.0b) de PEAR dont le lien est disponible en fin d'article.
Il utilise les extensions PHP de gestion de grands nombres. BCMath par défaut (la plus lente, mais la plus courante), BigInt ou GMP (classées ici de la plus lente à la plus rapide).
Elle est compatible PHP4 et PHP5.

J'y ai apporté quelques modifications. Ces modifications sont visibles dans les annexes.
Le but principal de ces modifications est de permettre la transmission de PHP vers JS et inversement en utilisant des nombres et non des hiéroglyphes.

Côté Javascript

À l'image du package Crypt_RSA de PEAR, j'ai utilisé une bibliothèque de gestion de grands nombres auquel j'ai ajouté quelques fonctions nécessaires pour coller avec notre modèle en PHP.
Finalement, on a deux fonctions principales. Une pour charger notre clé publique créée par PHP, l'autre pour encrypter.

function RSAPublicKey(encryptionExponent, modulus, nbBits)
function encryptedString(key, s)

Utilisation

Procédons par ordre chronologique. Tout d'abord, il nous faut générer les clés. Si vous vous souvenez bien, ceci est la charge du serveur, donc de Crypt_RSA.

set_include_path('./PEAR/');

session_start();

// Le package Crypt_RSA de PEAR
require_once 'Crypt/RSA.php';

// Les modifs apportées sur ce package
require_once './class/myKey.php';
require_once './class/myKeyPair.php';
require_once './class/myRSA.php';

$nbBits = 128; 
$key_pair = new Crypt_RSA_KeyPair($nbBits, 'BCMath');
$public_key = $key_pair->getPublicKey();
$private_key = $key_pair->getPrivateKey();
    
// on met en session la clé privée
$_SESSION['private_module'] = $private_key->getModulus();
$_SESSION['private_exp'] = $private_key->getExponent();

Remarquez que nous mettons la clé privée en session.

Il nous faut maintenant passer la clé publique au Javascript.

<script language="JavaScript" src="./js/BigInt.js"></script>
<script language="JavaScript" src="./js/BigIntMath.js"></script>
<script language="JavaScript" src="./js/RSA.js"></script>
<script language="JavaScript">
var key;
var EncryptedText;

// La clé publique passée aux js
var public_exponent = "<?php écho $public_key->getIntExponent(); ?>";
var public_modulus =  "<?php écho $public_key->getIntModulus(); ?>";

var nb_bits = <?php echo $nbBits; ?>;

// Initialisation de BigInt
setMaxDigits(154);

// Création de la clé publique
public_key = new RSAPublicKey(public_exponent, public_modulus, nb_bits);

Nous définissons maintenant deux fonctions, l'une pour récupérer la valeur saisie par l'utilisateur, la chiffrer et la replacer dans le champ (en modifiant légèrement les propriétés du champ au passage), l'autre pour annuler le chiffrement.

function encrypt()
{
    var code_str = document.register.codesecret.value;
    EncryptedText = encryptedString(public_key, code_str);
    document.register.codesecret.type='text';
    document.register.codesecret.size=EncryptedText.length; 
    document.register.codesecret.value=EncryptedText;
    document.register.isCrypted.value=1;
}

function annule()
{
    document.register.codesecret.type='password';
    document.register.codesecret.size=15; 
    document.register.codesecret.value='';
    document.register.isCrypted.value=0;
}

Enfin, il nous faut un formulaire utilisateur classique.

<form id="register" method="post" action="" name="register">
    <fieldset>
        <legend>Saisissez votre code secret</legend>
        <div>
            <label>
                <strong>Code secret : </strong><br />
                <input type="password" name="codesecret" size="16" autocomplete="off"/><br />
            </label>
        </div>
        <br />
        <input type="button" value="Chiffrer votre code secret" onclick="encrypt()" class="bouton">
        <input type="button" value="Annuler le chiffrement" onclick="annule()" class="bouton">
        <input type="hidden" name="isCrypted" value="0">
    </fieldset>
    <p align="center"><input type="submit" name="register" value="Valider" class="bouton" /></p>
</form>

Rien d'exceptionnel, juste à noter un champ caché qui permettra au PHP de savoir si le champ est chiffré ou non.

Et pour finir, la récupération du formulaire, avec le déchiffrement du champ si besoin.

if ( ! empty($_POST['codesecret']))
{
    $codesecret = $_POST['codesecret'];
    if ( (isset($_POST['isCrypted'])) && ($_POST['isCrypted'] == 1) )
    {
        $rsa_obj = new Crypt_RSA(null, 'BCMath');
        $private_key = new Crypt_RSA_Key($_SESSION['private_module'], $_SESSION['private_exp'], 'private', 'BCMath');
        $codesecret = $rsa_obj->decrypt($codesecret, $private_key);
    }
    
    echo 'Votre code secret : '.$codesecret;
}

Pour reconstituer cet exemple, il vous faudra :
- [ Les sources de l'exemple ].
- [ Le package PEAR ]
- [ Le package Crypt_RSA ]

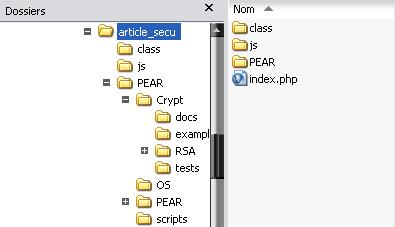
Renommez les répertoires de PEAR et Crypt_RSA de façon à obtenir cette arborescence.